0章:序章
0.1研究背景
0.1.1レシプロカル構造と現代性
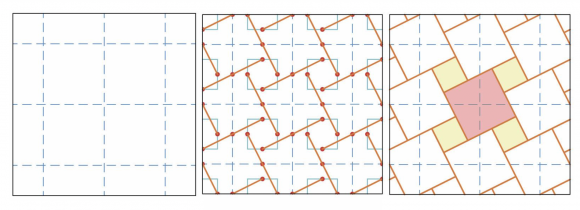
レシプロカル構造とは接合部に多くの部材が集中することを避け,部材同士が互いに支え合うことにより立体的に釣り合いを保つ構造であり、近年3DCADの普及により複雑な接合部も正確に設計できるようになった為再び注目を集めている。レシプロカル構造は小さな部材の組み合わせで大空間を構成することができる為、今後も普及していくことが予想されるが、レシプロカル構造の幾何学的な組み方はどのように導き出されるか具体的に定義されておらず、既存の建築も同じパターンを用いることが多くなってしまっている。
0.1.2推進される木造建築と未利用材の現状
2010年に「公共建築物等における木造の利用の推進に関する法律」が成立し公共建築の木造率が増加している。
一方で未利用材は全国で毎年、東京ドーム16個分に相当する2000万㎥分発生しており、その9割が伐採されたまま山間部で野ざらしとなっている。そもそも未利用材とは間伐や主伐により伐採された木材のうち未利用のまま林地に残置されている間伐材や災害などで発生する成長途中の小径材や根曲り材など一般的に流通されにくい材の総称である。未利用材が利用されにくいことには理由があり、部材の長さが規定よりも短いことや、断面が小さすぎて建材として利用できない為である。
0.2研究目的
この研究は今までにない幾何学パターンを用いたレシプロカル構造を新たに導き出すことを目的としている。さらに平面充填の多角形からレシプロカル構造を導き出す方法を定義することで誰もが利用できる構造とし、普及につなげる。また、新たなレシプロカル構造としてペンローズタイルなどの非周期的幾何学から導く。これらのレシプロカル構造を建築に落とし込み、未利用材を建材として用いることで未利用材の新たな利用価値を見出すことを最終的な目的としている。
0.3研究の位置付け
1種類のみで平面を充填することができる正多角形は三角形、四角形、六角形であり、既往研究ではそれら3つをグリットとしてレシプロカル構造を導き出していた。
また、レシプロカル構造を建築に用いている事例は国内で数えられるほどしか確認されていない。しかし幾何学的に平面を充填させる方法は数え切れないほど存在している。
未だに建築に落とし込まれていない幾何学パターンの中から新たなレシプロカルフレームを導く。また、ペンローズタイルのような非周期的幾何学を用いたレシプロカル構造はどのようなものになるのか考察する。未利用材の有効活用法としてチップに加工することが現在の主流な方法として行われているが、森林系のチップは廃木材系のチップに比べて森林燃料の調達コストがあまりにも高く、利用が進んでいないという現状がある。
0.4研究方法
この研究では無限に存在する平面充填の幾何学の中から、多角形の配置により分類を行い、「部材の種類、部材のサイズ差、意匠性」などの特性を比較検討していく。レシプロカル構造を使うことで建材の規格から外れ未利用材となってしまっていた最小径14cm以下の小径材や災害などによって発生した不揃いな断面を持つ木を建材として利用し、再利用の可能性を探る。設計対象は、木造化を推進している公共建築である府中第一中学校の体育館とし、30m角正方形平面にかける屋根の架構を提案する
1章:平面充填する周期的な多角形を用いたレシプロカル構造
1.0配置
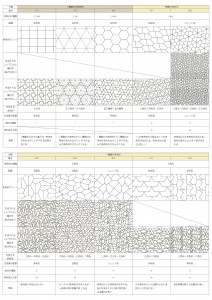
多角形の配置の仕方にはいくつかのパターンがある。それらを分類することで無限に存在する幾何学の中から一定数の幾何学に絞ることができる。「並列型・斜め型・回転型・ユニット型」の4つの配列に分類を行い、いずれかに当てはまらないものを「その他」とした。これによって元の多角形と生成される多角形でどのように配置が変わるのかを考察することができる。
1.1一種類の正多角形による平面充填
一種類の正多角形で平面充填が可能である三角形、四角形、六角形におけるレシプロカルフレームの生成を行う。
1.2一種類の多角形による平面充填
平面充填できる一種の多角形で有限に存在する五角形と無限に存在する七角形から配置分類を参考に選定し、いくつかの多角形を用いてレシプロカルフレームの生成を行う。
1.3複数の多角形による平面充填
複数の多角形による平面充填幾何学からレシプロカルフレームを生成する。その中でも正多角形のみのもの、正多角形を含むもの、正多角形を含まないものに分類できる。
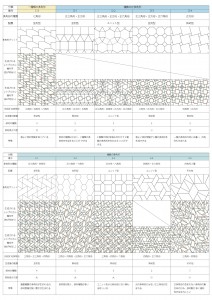
2章:非周期的幾何学を用いたレシプロカル構造
2.1非周期的幾何学とは
非周期的幾何学は周期的に配列すると平面充填が不可能なため、強制的に非周期的に配列せざるを得ないのである。
2.2ペンローズタイル
ペンローズ・タイルとは、イギリスの物理学者ロジャー・ペンローズが考案した平面充填形で二種類の菱形によるものである。菱形と三角形で構成されるものの二種類があり、両方のパターンでレシプロカルフレームの生成を試みる。
3章:未利用材を用いたレシプロカル構造
3.1種類と材料特性
間伐や主伐により伐採された木材のうち未利用のまま林地に残置されている間伐材や枝条等や、災害などで発生する成長途中の小径材や根曲り材など一般的に流通されにくい材の総称を「未利用材」と呼ぶ。
3.2レシプロカル構造と未利用材の選定
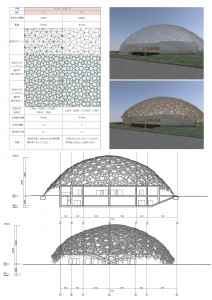
1章2章で導き出したレシプロカル構造の中から30m角の正方形平面を持つ体育館に適した架構と、用いる部材の検討を行う。体育館の仮構として意匠性が高いことやユニット化されており接合部の検討がしやすいもの、未利用材の利用がしやすいような部材長さが短くて済み曲げ材などを用いることが可能なものなど様々な条件から判断していく。そのためにまずこれまでに生成したレシプロカル構造を表にまとめ、上記の条件から五角形の平面充填の多角形から生成されたB-2を用いることとする。(一覧表参照)架構の構成部材としては流通材の他に未利用材の一種である小径材と曲げ材を用いることとした。
3.3接合部の検討
曲率が変わることを防ぐため体育館の架構の形は正円ドームとする。レシプロカル構造は3DCADの普及によって接合部の検討がしやすくなったとはいえ接合部の角度が全て変わってしまうことは施工しづらい。ユニット型の特徴を踏まえつつ接合部の検討を行う。
3.4考察
レシプロカル構造によって小さな部材で大空間を生み出すことができた。曲げ材が入ることによって空間に変化が生まれ、ある程度の規則性があることによって複雑だが整った印象の空間となる。以前自身で設計した平面プランと変わらないにもかかわらず変化のあるダイナミックな印象を受ける。また、接合部の角度がほとんど同じで構成できるという利点があったためモデリングも容易かった。これは施工のしやすさと捉えられるだろう。
4章:結章
4.1総括
今まであまり建築で用いられてこなかったレシプロカル構造を、平面充填の幾何学から生み出すという方法により新しいレシプロカルフレームを生成することによって建築に落とし込むことができた。生成された建築空間は短い材で30m角の大空間の架構を作りだし、意匠性の高いダイナミックな空間で、規則性の中にも複雑さが垣間見るようなレシプロカル構造でしか作り出すことのできないものとなった。また、過剰な伐採や災害などで問題視されている未利用材の有効活用法を提案した。レシプロカル構造を用いて意図的に断面にばらつきの生まれる構造とすることで今まで建材として利用されてこなかった不揃いな断面を持つ未利用材を、大空間を構成する部材として再定義する。
4.2展望
この研究では実際にモデル化することで規格化により誰もが簡単に施工できるようになることを示すことができたが、具体的な接合部の金物の設計まで落とし込むことができなかった。レシプロカル構造に適応した接合部ができるとさらなる普及につながるであろう。また、無限に存在する平面充填の幾何学の中で今回選定した数十種はほんの一部に過ぎない。レシプロカルフレームの生成アリゴリズムが普及すれば、今回用いられなかったものを含め平面充填から生み出されるレシプロカルフレームが今後建築に落とし込まれていく未来を期待したい。
[参考文献]
・「アルゴリズムを用いたレシプロカルフレーム構造による地域図書館の構造デザイン」(修士設計)/東京電機大学大学院 清水秀太郎
・感度解析によるレシプロカル構造の位相最適化に関する研究(荷重・応答予測、構造Ⅲ、学術講演会・建築デザイン発表会)/櫻井昭宏・佐々木睦朗・浜田英明
・Multiple Reciprocal Frame構造による木造屋根架構の提案(修士設計)/東京理科大学大学院工学研究科建築学専攻 志村亮
・ジオメトリックエンジニアリング(第36回情報・システム・利用・技術シンポジウム2013)/城所竜太・後藤一真・天野裕















 ARCHIVES
ARCHIVES コンペ
コンペ 南方熊楠研究所2003
南方熊楠研究所2003 城下町2005
城下町2005 岩見沢駅舎2005
岩見沢駅舎2005 立川市新庁舎2005
立川市新庁舎2005 PROJECT&RESEARCH
PROJECT&RESEARCH WKH2005
WKH2005 北京ワークショップ2012
北京ワークショップ2012 修士設計2010
修士設計2010 コンピューテーショナルデザイン
コンピューテーショナルデザイン テクトニクスと建築
テクトニクスと建築 中国の現代集合住宅
中国の現代集合住宅 伝統的集落
伝統的集落 卒業設計リスト
卒業設計リスト